Competitive insurance pricing using model-based bandits

Date: 12.06.2024

Summary of my paper "Competitive Insurance Pricing Using Model-Based Bandits" written with my supervisors David Siska, Lukasz Szpruch and co-author Tanut Treetanthiploet.

The main goal of the paper was to explore using Bayesian bandit algorithm with a logistic model to compete within a pricing environment.

The full paper is available at https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4755027.

Modelling the probability of conversion

In many pricing environments, the probability of conversion - the probability that the offer will be accepted by the customer - is often believed to follow a logistic curve where the price offered to the customer enters as a feature. As en exaple, consider an environment where customer's reservation price - the boundary after which they will accept the offer is a normally distributed with some mean and variance. Then, the probability of conversion is effectively a resized normal distribution cdf (cumulative distribution function) - see figure below.

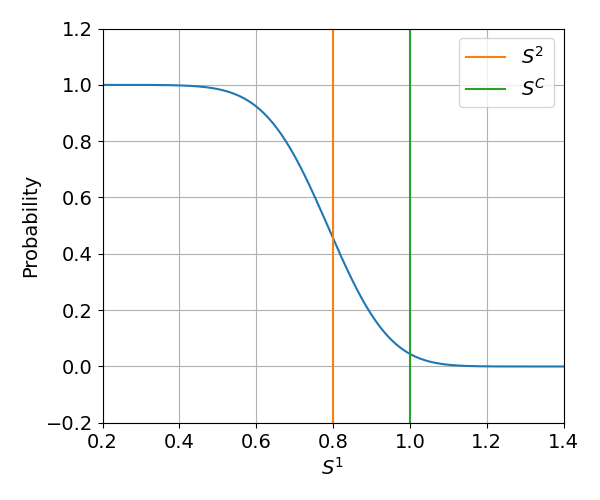
Cdf of normal ditribution

Such function can be quite accurately approximated with a logistic curve with equation:

$$ p(x) = \frac{1}{1 + \exp(\beta_0 + \beta_1 \cdot x)}, $$

where the $x$ is a price and $\beta_0, \beta_1$ are some parameters.

Often, the environment used for numerical simulations is explicitly logistic in which case the logistic curve exactly represents the environment.

Does the model help the bandit?

Since the model approximates the environment, we would expect that the bandits endowed with the model information would outperform naive classical bandit algorithms such as epsilon greedy classical bandit. Epsilon-greedy bandit algorithm explores available actions with a constant rate and regards each action (in this case price) as independent from each other. Each action is believed to return a reward sampled from a normal distribution with unknown mean and known variance. This is clearly very different from the actual model.

Goal of the project

Thus, the main goal of the project was to run numerical experiments of pricing competition using different model-based and naive bandits algorithms and compare their performance.

Defining performance

When we want to compare the bandits, we have to carefully define the performance metric by which to judge the algorithms. In the paper, we run three sets of experiments:

  • Expected cumulative reward in a stationary environment.
  • Expected cumulative reward in a non-stationary environment, where the action of the opponent experiences sudden changes every fixed number of time steps.
  • Expected cumulative reward in a direct competition between bandit algorithms. In this case, we run experiments where one bandit is already within the environment and the other one enters and causes a disruption.

Bandit algorithms

The numerical experiments were run with various bandit algorithms. The bandit algorithms were split according to following characteristics:

  • Used model - logistic vs. classic - the logistic bandits used the logistic model of the environment while the classic bandits used the "classic" model with independent, normally distributed rewards.
  • Stationarity - stationary vs non-stationary - for the competition in a fixed environment, the bandit algorithms were stationary; for the non-stationary tests and the competition between bandit algorithms, the algorithms were non-stationary. Specifically, the non-stationary algorithms used sliding-window approach - the observations older than some fixed number of steps were discarded and not used to compute the optimal action.
  • Decision rule - the exploration policy. In the paper we used UCB and epsilon-greedy but here we will discuss epsgreedy only as UCB did not perform well in non-stationary settings.

Environment

In the environment, each new step corresponded to a new customer. At each step, each agent estimated the cost of the client. the estimates followed a multivariate normal distribution. Furthermore, each client has a reservation price sampled from a normal distribution.

Each agent submitted a margin which was added to the cost estimate - the sum was then regarded as a price offered by the agent. Then, the offer with the smallest price was accepted as long as it was smaller than the customer reservation price.

The agent whose offer was accepted received a reward equal to the proposed margin. For more details about the environment, see the original paper.

Numerical experiments conducted indicated that the environment above is well approximated using logistic regression.

Results

I will focus on the main conclusions of the study.

Conclusion 1: Model helps for stationary competition

Providing a correct or approximately correct model to the bandit algorithm can improve the performance of the bandit. Effectively, the model allows the bandit to find the optimal action more quickly. Figure below presents the average reward of the classic bandit over the episode and the figure after presents the same plot for the logistic agent. The logistic agent finds the optimal action almost instantly. In the experiments below, the agents were competing against an adversary with a fixed action and thus the environment was stationary.

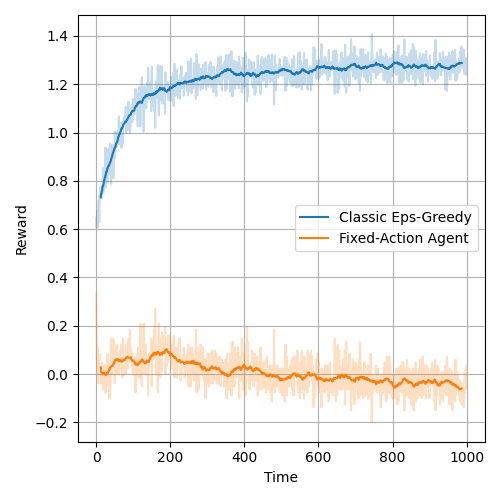
epsgreedy_classic_vs_fixed_action

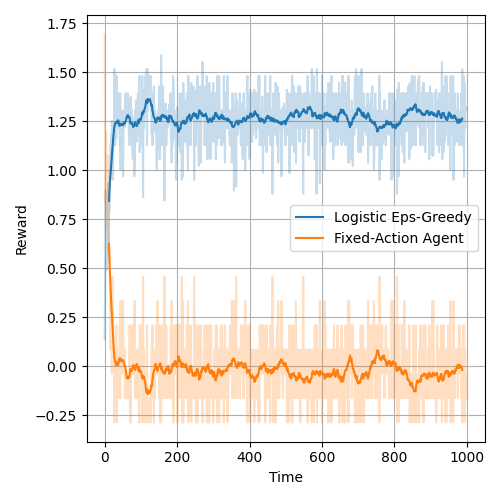
epsgreedy_logistic_vs_fixed_action

It is also worth noting, that using UCB for exploration/exploitation policy further improved the achieved reward.

Conclusion 2: Model might provide advangtage in a non-stationary environment

When the fixed-action agent is replaced with an agent whose action changes drastically every number of steps, the advantage of model-based bandits is diminished. In this case, the bandits were non-stationary. Observations older than around 50 steps were discrarded.

While the model helped to find the correct reward after the opposing agent changed their action, for a number of steps the action chosen by the logistic agent was more suboptimal than classical bandit's action. Furthermore, the forgetting of the past observations negatively affects the logistic model - the model becomes naturally regularized and favors actions corresponding to higher prices which generally perform much worse. Figures below present the reward plots for the classic and logistic bandits respectively in a environment with an opponent with fluctuating action. The opponent action followed a square wave - the price changed from 0.3 to 0.7 every 250 steps.

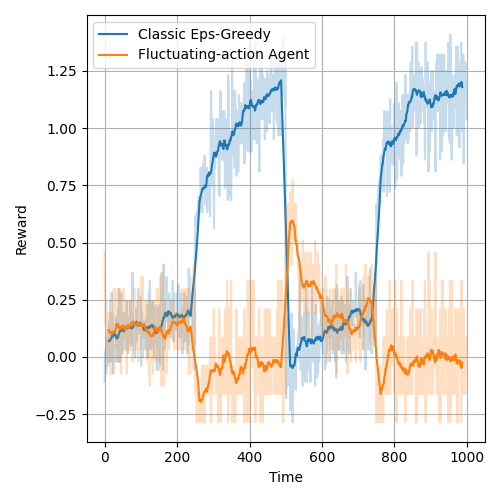
classic_vs_fluctuating

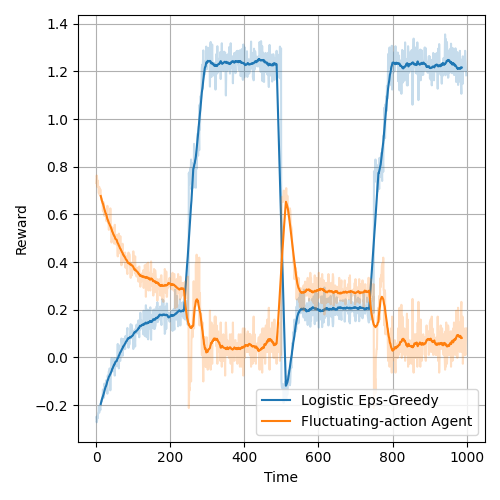
logistic_vs_fluctuating

The UCB bandits suffered from the optimism principle and underperformed.

Conclusion 3: Model provides no advantage for price competitions between learning bandits

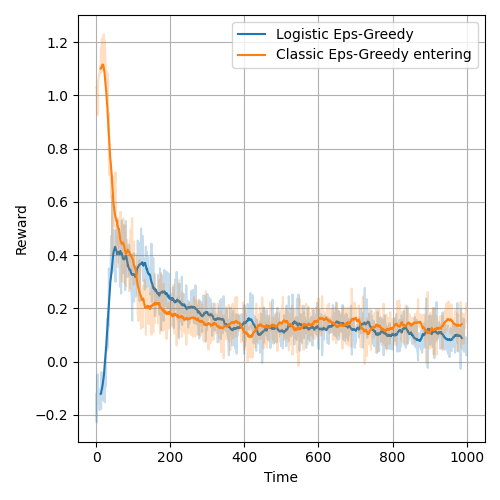
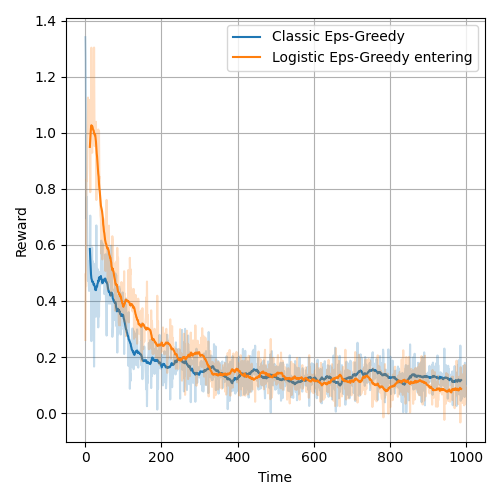
In the price competitions where one bandit was entering the pricing environment with the other bandit present, the logistic model provides no advatage to the bandit model.

The competing bandit learns rapidly and explores randomly which causes the environment to be poorly represented by the logistic model - since the model no longer approximates the environment, the advantage is lost. Rather, the logistic bandit is at disadvantage which is further exacerbated by the previously mentioned regularisation of the logistic model due to observation forgetting.

Figure below presents average rewards from a pricing competition where the logistic bandit enters the pricing environment with the classic bandit. In the figure after, the roles are exchanged - the classic bandits enters and disrupts the logistic bandit.

classic_enters_logistic

logistic_enters_classic

Summary

The main conclusion to take from the project is the model of the environment is only useful when it accurately represents the environment, including the agents which might be learinng and adjusting their action.

In this case, the standard epsilon-greedy classical bandit algorithm is a robust option for learing in an unknown multi-agent environment.

Any questions or comments are welcomed. Please reach out using the contact information.